The limit of sinx/x as x approaches 0 is 1, that is, the limit formula of sinx/x when x tends to 0 is given by
limx→0 $\dfrac{\sin x}{x} = 1$.
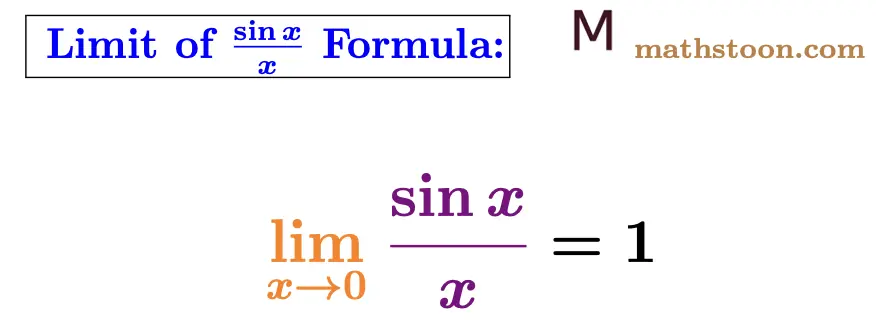
Let us now prove that the limit of sinx/x is equal to 1 when x goes to 0.
Table of Contents
Limit of sinx/x as x→0 by Sandwich or Squeeze Theorem
Prove that limx→0 $\dfrac{\sin x}{x} = 1$.
Solution:
We know that for all real values of x,
sin x ≤ x and x ≤ tan x.
This implies that
sin x ≤ x ≤ tan x
Dividing by sinx we get that
$1 \leq \dfrac{x}{\sin x} \leq \dfrac{\tan x}{\sin x}$
⇒ $1 \leq \dfrac{x}{\sin x} \leq \dfrac{1}{\cos x}$ as we know tanx=sinx/cosx.
Now, taking the limit x→0 on both sides we get that
limx→0 1 ≤ limx→0 $\dfrac{x}{\sin x}$ ≤ limx→0 $\dfrac{1}{\cos x}$
⇒ 1 ≤ limx→0 $\dfrac{x}{\sin x}$ ≤ $\dfrac{1}{\cos 0}$
⇒ 1 ≤ limx→0 $\dfrac{x}{\sin x}$ ≤ 1 as the value of cos0 is 1.
So by the Squeeze theorem of limits, we conclude that
limx→0 $\dfrac{x}{\sin x}$ = 1
By the division rule of limits,
limx→0 $\dfrac{\sin x}{x}$ = 1.
So the value of the limit of sinx/x is equal to 1 when x tends to 0, and it is obtained by the Squeeze theorem (or Sandwich theorem) of limits.
Main Article: Limit: definition, formulas and examples
limx→∞ (sinx/x) Formula, Proof
Lim x→0 sinx/x by l’Hopital’s Rule
To find the value of limx→0 sinx/x, first notice that $\dfrac{\sin 0}{0}=\dfrac{0}{0}$, so the given limit is an indeterminate form. Thus, by l’Hopital’s rule, we have that
limx→0 $\dfrac{\sin x}{x}$
= limx→0 $\dfrac{(\sin x)’}{x’}$ where $’$ denoted the first order derivative with respect to x.
= limx→0 $\dfrac{\cos x}{1}$
= limx→0 cosx
= cos 0
= 1.
Hence the limit of sinx/x by l’Hopital’s rule is equal to 1 when x approaches 0.
You can read: Proofs of all Limit Properties
Solved Examples
Now, as an application of the limit formula of sinx/x when x tends to zero, we will evaluate a few limits.
| Question 1: Find the limit of sin2x/x when x tends to 0, that is, Find limx→0 $\dfrac{\sin 2x}{x}$. |
Answer:
limx→0 $\dfrac{\sin 2x}{x}$
= limx→0 $\Big( \dfrac{\sin 2x}{2x} \times 2 \Big)$
=2 limx→0 $\dfrac{\sin 2x}{2x}$
[Let t=3x. Then t→0 when x→0]
=2 limx→0 $\dfrac{\sin t}{t}$
=2 × 1 as the limit of sinx/x is 1 by above when x→0.
=2
So the limit of sin2x/x is equal to 2 when x tends to 0.
| Question 2: Find the limit of sin3x/x when x tends to 0, that is, Find limx→0 $\dfrac{\sin 3x}{x}$. |
Answer:
limx→0 $\dfrac{\sin 3x}{x}$
= limx→0 $\Big( \dfrac{\sin 3x}{2x} \times 3 \Big)$
=3 limt→0 $\dfrac{\sin t}{t}$, where t=3x, so that t→0 when x→0
=3 × 1 = 3.
Therefore, the limit of sin3x/x is equal to 3 when x tends to 0.
| Question 3: Find the limit of sin3x/sin2x when x tends to 0, that is, Find limx→0 $\dfrac{\sin 3x}{\sin 2x}$. |
Answer:
limx→0 $\dfrac{\sin 3x}{\sin 2x}$
= limx→0 $\Big( \dfrac{3}{2} \times \dfrac{\sin 3x}{3x} \times \dfrac{2x}{\sin 2x} \Big)$
= $\dfrac{3}{2}$ limx→0 $\dfrac{\sin 3x}{3x}$ limx→0 $\dfrac{2x}{\sin 2x}$ by the properties of limits.
[Let t=3x and z=2x. Then both t, z→0 when x→0]
= $\dfrac{3}{2}$ × 1 × $\dfrac{1}{\lim\limits_{z \to 0}\frac{\sin z}{z}}$
= $\dfrac{3}{2}$ × 1 × $\dfrac{1}{1}$
= $\dfrac{3}{2}$.
So the limit of sin3x/2x is equal to 3/2 when x tends to 0.
FAQs
Answer: The limit of sinx/x when x→0 is equal to 1. In other words, limx→0 sinx/x = 1.
Answer: The value of limx→0 sinx/x is equal to 1.
Answer: The limit of sin2x/x when x→0 is equal to 2. That is, limx→0 sin2x/x = 1.
Answer: The limit of sin3x/x when x→0 is equal to 3. That is, limx→0 sin3x/x = 1.
Answer: The limit of sin2x/sin3x is equal to 2/3 when x tends to 0.
Answer: The limit of sin3x/sin2x is equal to 3/2 when x tends to 0.
This article is written by Dr. T, an expert in Mathematics (PhD). On Mathstoon.com you will find Maths from very basic level to advanced level. Thanks for visiting.