Limit of sinx/x as x approaches 0: Formula, Proof

The limit of sinx/x as x approaches 0 is 1, that is, the limit formula of sinx/x when x tends to 0 is given by

lim_x→0 $\dfrac{\sin x}{x} = 1$.

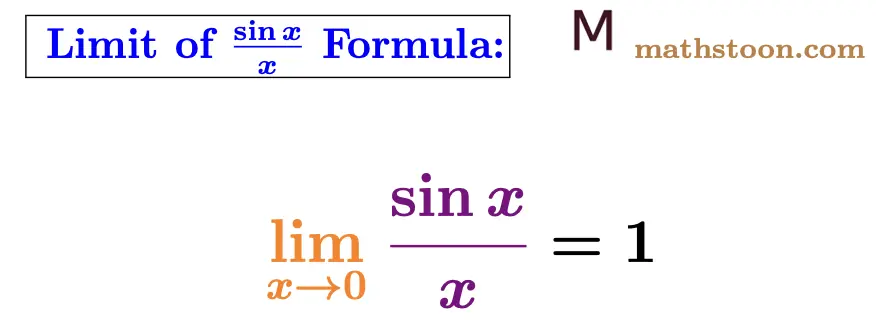
Let us now prove that the limit of sinx/x is equal to 1 when x goes to 0.

Limit of sinx/x as x→0 by Sandwich or Squeeze Theorem

Prove that lim_x→0 $\dfrac{\sin x}{x} = 1$.

Solution:

We know that for all real values of x,

sin x ≤ x and x ≤ tan x.

This implies that

sin x ≤ x ≤ tan x

Dividing by sinx we get that

$1 \leq \dfrac{x}{\sin x} \leq \dfrac{\tan x}{\sin x}$

⇒ $1 \leq \dfrac{x}{\sin x} \leq \dfrac{1}{\cos x}$ as we know tanx=sinx/cosx.

Now, taking the limit x→0 on both sides we get that

lim_x→0 1 ≤ lim_x→0 $\dfrac{x}{\sin x}$ ≤ lim_x→0 $\dfrac{1}{\cos x}$

⇒ 1 ≤ lim_x→0 $\dfrac{x}{\sin x}$ ≤ $\dfrac{1}{\cos 0}$

⇒ 1 ≤ lim_x→0 $\dfrac{x}{\sin x}$ ≤ 1 as the value of cos0 is 1.

So by the Squeeze theorem of limits, we conclude that

lim_x→0 $\dfrac{x}{\sin x}$ = 1

By the division rule of limits,

lim_x→0 $\dfrac{\sin x}{x}$ = 1.

So the value of the limit of sinx/x is equal to 1 when x tends to 0, and it is obtained by the Squeeze theorem (or Sandwich theorem) of limits.

Main Article: Limit: definition, formulas and examples

Lim x→0 sinx/x by l’Hopital’s Rule

To find the value of lim_x→0 sinx/x, first notice that $\dfrac{\sin 0}{0}=\dfrac{0}{0}$, so the given limit is an indeterminate form. Thus, by l’Hopital’s rule, we have that

lim_x→0 $\dfrac{\sin x}{x}$

= lim_x→0 $\dfrac{(\sin x)’}{x’}$ where $’$ denoted the first order derivative with respect to x.

= lim_x→0 $\dfrac{\cos x}{1}$

= lim_x→0 cosx

= cos 0

= 1.

Hence the limit of sinx/x by l’Hopital’s rule is equal to 1 when x approaches 0.

You can read: Proofs of all Limit Properties

Proofs of all Limit formulas

Solved Examples

Now, as an application of the limit formula of sinx/x when x tends to zero, we will evaluate a few limits.

Question 1: Find the limit of sin2x/x when x tends to 0, that is, Find limx→0 $\dfrac{\sin 2x}{x}$.

Answer:

lim_x→0 $\dfrac{\sin 2x}{x}$

= lim_x→0 $\Big( \dfrac{\sin 2x}{2x} \times 2 \Big)$

=2 lim_x→0 $\dfrac{\sin 2x}{2x}$

[Let t=3x. Then t→0 when x→0]

=2 lim_x→0 $\dfrac{\sin t}{t}$

=2 × 1 as the limit of sinx/x is 1 by above when x→0.

=2

So the limit of sin2x/x is equal to 2 when x tends to 0.

Question 2: Find the limit of sin3x/x when x tends to 0, that is, Find limx→0 $\dfrac{\sin 3x}{x}$.

Answer:

lim_x→0 $\dfrac{\sin 3x}{x}$

= lim_x→0 $\Big( \dfrac{\sin 3x}{2x} \times 3 \Big)$

=3 lim_t→0 $\dfrac{\sin t}{t}$, where t=3x, so that t→0 when x→0

=3 × 1 = 3.

Therefore, the limit of sin3x/x is equal to 3 when x tends to 0.

Question 3: Find the limit of sin3x/sin2x when x tends to 0, that is, Find limx→0 $\dfrac{\sin 3x}{\sin 2x}$.

Answer:

lim_x→0 $\dfrac{\sin 3x}{\sin 2x}$

= lim_x→0 $\Big( \dfrac{3}{2} \times \dfrac{\sin 3x}{3x} \times \dfrac{2x}{\sin 2x} \Big)$

= $\dfrac{3}{2}$ lim_x→0 $\dfrac{\sin 3x}{3x}$ lim_x→0 $\dfrac{2x}{\sin 2x}$ by the properties of limits.

[Let t=3x and z=2x. Then both t, z→0 when x→0]

= $\dfrac{3}{2}$ × 1 × $\dfrac{1}{\lim\limits_{z \to 0}\frac{\sin z}{z}}$

= $\dfrac{3}{2}$ × 1 × $\dfrac{1}{1}$

= $\dfrac{3}{2}$.

So the limit of sin3x/2x is equal to 3/2 when x tends to 0.

FAQs