The derivative of 1/x2 is equal to -2/x3. In this article, we will learn how to find the derivative of 1 divided by x2 using the power rule, product rule, and the definition of derivatives.
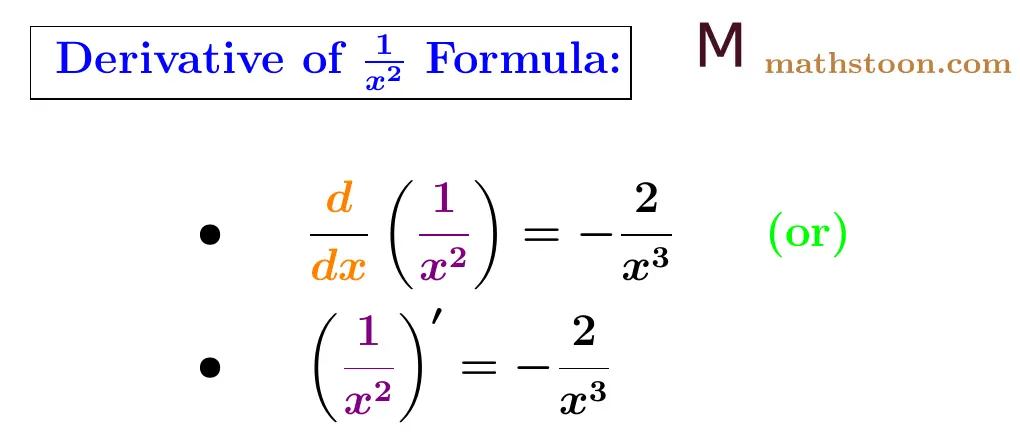
Table of Contents
Derivative of 1/x2 Formula
Note that 1/x2 is an algebraic function. The derivative of 1/x2 can be expressed as d/dx(1/x2) or (1/x2)$’$. The derivative formula of 1 divided by x square is given below:
d/dx(1/x2) = -2/x3 or (1/x2)$’$ = -2/x3.
What is the Derivative of 1/x2?
Derivative of 1/x2 by power rule: Let us first find the derivative of 1 by x2 by the power rule of derivatives. Recall the power rule of derivatives: d/dx(xn) = nxn-1.
Follow the below steps to find the differentiation of 1 divided by x2.
| Express 1/x2 as a power of x | 1/x2 = x-2 |
| Differentiate both sides w.r.t. x | d/dx(1/x2) = d/dx(x-2) |
| Apply the power rule of derivatives | d/dx(1/x2) = d/dx(x-2) = -2x-2-1 |
| Simplify | ∴ d/dx(1/x2) = -2x-3 = -2/x3 |
Conclusion: The derivative of 1/x2 by power rule is -2/x3.
Derivative of 1/x2 by First Principle
If f(x) is a function of real variable x, then the derivative of f(x) by the first principle is given by the following limit formula:
$\dfrac{d}{dx}(f(x))$ = limh→0 $\dfrac{f(x+h)-f(x)}{h}$
Put f(x) = 1/x2
So the derivative of 1/x2 from first principle is
$\dfrac{d}{dx}\big(\dfrac{1}{x^2} \big)$ = limh→0 $\dfrac{\frac{1}{(x+h)^2}-\frac{1}{x^2}}{h}$
= limh→0 $\dfrac{x^2-(x+h)^2}{hx^2(x+h)^2}$
= limh→0 $\dfrac{x^2-(x^2+2xh+h^2)}{hx^2(x+h)^2}$
= limh→0 $\dfrac{-h(2x+h)}{hx^2(x+h)^2}$
= limh→0 $\dfrac{-(2x+h)}{x^2(x+h)^2}$
= $\dfrac{-(2x+0)}{x^2(x+0)^2}$
= $\dfrac{-2x}{x^4}$ = $-\dfrac{2}{x^3}$.
Thus, the derivative of 1/x2 is equal to -2/x3 and this is obtained from the first principle of derivatives.
Also Read:
| Derivative of 1/x: | -1/x2 |
| Derivative of tan x: | sec2x |
| Derivative of esin x : | cos x esin x |
| Derivative of log 2x: | 1/x |
Derivative of 1/x2 by Product Rule
Now, we will find the derivative of 1/x2 by the substitution method together with the product rule of derivatives. For this let us put
z=1/x2. We need to find dz/dx.
This implies that
zx2=1
Differentiating with respect to x, we get that
$\dfrac{d}{dx}(zx^2)=\dfrac{d}{dx}(1)$
⇒ $z\dfrac{d}{dx}(x^2)+x^2\dfrac{d}{dx}(z)=0$ (by the product rule of derivatives)
⇒ z⋅2x + x2 $\dfrac{dz}{dx}$ = 0
⇒ $x^2\dfrac{dz}{dx}=-2zx$
⇒ $\dfrac{dz}{dx}=-\dfrac{2z}{x}$
⇒ $\dfrac{dz}{dx}=-\dfrac{2}{x^3}$ as z=1/x2
So we have obtained the differentiation of 1/x2 by the product rule which is -2/x3.
Also Read: How to Differentiate 1/x3?
Solved Problems
Question: Find the derivative of 1/sin2x.
Answer:
Let z=sinx.
So dz/dx = cosx.
So by the chain rule, the derivative of 1/sin2x is equal to
d/dx (1/sin2x)
= $\dfrac{d}{dz}(\dfrac{1}{z^2}) \times \dfrac{dz}{dx}$
= $-\dfrac{2}{z^3} \times \cos x$, by the above differentiation rule of 1/x2.
= $-\dfrac{2\cos x}{\sin^3 x}$ as z=sinx.
So the derivative of 1/sin2x is equal to -2cosx/sin3x, obtained by the chain rule of derivatives.
FAQs on Derivative of 1/x2
Answer: The derivative of 1/x2 (1 over x square) is equal to -2/x3.
Answer: The derivative of x2 (x square) is 2x.
This article is written by Dr. T, an expert in Mathematics (PhD). On Mathstoon.com you will find Maths from very basic level to advanced level. Thanks for visiting.