The divisors of 16 are 1, 2, 4, 8, and 16. The divisors of 16 are those numbers that completely divide 16 without a remainder. In this section, we will discuss about divisors of 16.
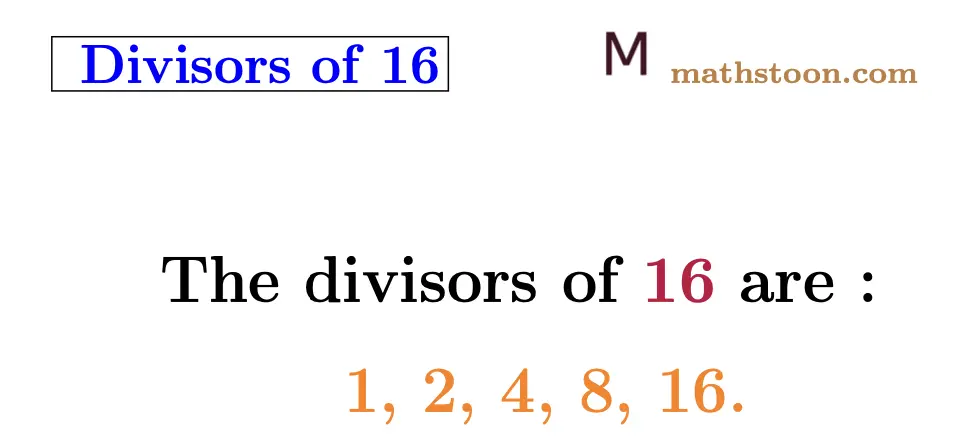
Table of Contents
Highlights of Divisors of 16
- Divisors of 16: 1, 2, 4, 8 and 16
- Negative divisors of 16: -1, -2, -4, -8 and -16
- Prime divisors of 16: 2
- Number of divisors of 16: 5
- Sum of divisors of 16: 31
- Product of divisors of 16: 165/2 = 45 =1024.
What are Divisors of 16
A number n is a divisor of 16 if $\dfrac{16}{n}$ is an integer. Note that if 16/n=m is an integer, then both m and n will be the divisors of 16.
To find the divisors of 16, we need to find the numbers n such that 16/n becomes an integer. We have:
| 16/1=16 | 1, 16 are divisors of 16. |
| 16/2=8 | 2, 8 are divisors of 16 |
| 16/4=4 | 4 is a divisor of 16 |
No numbers other than 1, 2, 4, 8, and 16 can divide 16. So we conclude that
| The divisors of 16 are: 1, 2, 4, 8, and 16. |
Properties of Divisors of 16
- The total number of divisors of 16 is five.
- Using the fact that if m is a divisor of a number, then -m is also a divisor of that number, we conclude that the negative divisors of 16 are -1, -2, -4, -8, and –16.
- Among the divisors of 16, only 2 is a prime number. So the only prime divisor of 16 is 2.
Sum, Product & Number of Divisors of 16
The prime factorization of 16 is given below.
16 = 24
(i) By the number of divisors formula, we have that the number of divisors of 16 is = (4+1) = 5.
(ii) By the sum of divisors formula, we have that the sum of the divisors of 16 is
$=\dfrac{2^5-1}{2-1}$
$=\dfrac{32-1}{1}$
= 31.
So the sum of divisors of 16 is equal to 31.
(iii) By the product of divisors formula, we have that the product of the divisors of 16 is
=16(Number of divisors of 16)/2
=165/2 as the number of divisors of 16 is 5.
=45
=1024.
So the product of divisors of 16 is equal to 1024.
Related Topics:
Video solution of Divisors of 16:
Problem Solution on Divisors of 16
Question 1: What is the set of all divisors of 16 in roster form?
Solution:
Note that only 1, 2, 4, 8, and 16 divide the number 16. Thus the set of all divisors of 16 in roster form is given as follows:
{1, 2, 4, 8, 16}.
Question 2: What is the set of all prime divisors of 16 in roster form?
Solution:
Only the prime number 2 can divide the number 16. Thus, the set of all prime divisors of 16 in roster form is the singleton set {2}.
This article is written by Dr. T, an expert in Mathematics (PhD). On Mathstoon.com you will find Maths from very basic level to advanced level. Thanks for visiting.