All Divisors of 60: What are the Divisors of 60

The divisors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. The divisors of 60 are those numbers that completely divide 60 without a remainder. In this section, we will discuss divisors of 60.

Highlights of Divisors of 60

• All Divisors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60
• Negative divisors of 60: -1, -2, -3, -4, -5, -6, -10, -12, -15, -20, -30 and -60
• Prime divisors of 60: 2, 3 and 5
• Number of divisors of 60: 12
• Sum of divisors of 60: 168
• Product of divisors of 60: 60⁶ 

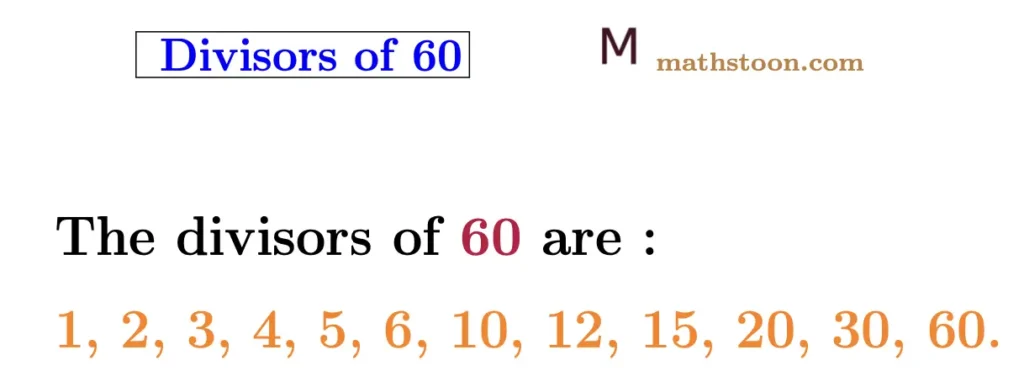
What are Divisors of 60

We say a number is a divisor of 60 if it divides 60 completely. Thus n is a divisor of 60 if $\dfrac{60}{n}$ is an integer. Therefore, to find the divisors of 60, we need to find the number n such that 60/n becomes an integer. We have:

60/1=60	1, 60 are divisors of 60.
60/2=30	2, 30 are divisors of 60.
60/3=20	3, 20 are divisors of 60
60/4=15	4, 15 are divisors of 60
60/5=12	5, 12 are divisors of 60
60/6=10	6, 10 are divisors of 60

No numbers other than 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60 can divide 60. So we conclude that the divisors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.

Thus, the total number of divisors of 60 is twelve.

Also Read:

Divisors of 64: The divisors of 60 are 1, 2, 4, 8, 16, 32, 64.

Divisors of 72: The divisors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.

Divisors of 75: The divisors of 75 are 1, 3, 5, 15, 25, 75.

Divisors of 100: The divisors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100.

Negative Divisors of 60

We know that if m is a divisor of a number, then -m is also a divisor of that number.

As the divisors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60, we can say that:

The negative divisors of 60 are -1, -2, -3, -4, -5, -6, -10, -12, -15, -20, -30, and -60.

Prime Divisors of 60

The divisors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. Among these numbers, only 2, 3, and 5 are prime numbers. So we obtain that:

The prime divisors of 60 are 2, 3, and 5.

Divisors of 60 Formula

The prime factorization of 60 is given below.

60 = 2² × 3¹ × 5¹

(i) By the number of divisors formula, we have that the number of divisors of 60 is

=(2+1)(1+1)(1+1)=3×2× 2=12.

(ii) By the sum of divisors formula, we have that the sum of the divisors of 60 is

$=\frac{2^3-1}{2-1} \times \frac{3^2-1}{3-1}$ $\times \frac{5^2-1}{5-1}$

$=\frac{8-1}{1} \times \frac{9-1}{2}$ $\times \frac{25-1}{4}$

$=7 \times 4 \times 6=168$

(iii) By the product of divisors formula, we have that the product of the divisors of 60 is

=60^{(Number of divisors of 60)/2}

=60^12/2

=60⁶

Related Topics:

• Divisors of numbers
• Factors of 60

Problem Solution on Divisors of 60

Question: Write the following sets in roster form 

D = {$x : x$ is a prime number which is divisor of 60}

Answer: Note that the set contains the prime numbers $x$ which are divisors of 60. Thus $x$ is a prime divisor of 60.

From the above, we know that the prime divisors of 60 are 2, 3, and 5.

∴ D = {2, 3, 5}

FAQs on Divisors of 60