Find Laplace transform of t^2 [t Square]

The Laplace transform of t^2, i.e the Laplace of t square is equal to 2/s³. In this article, we will learn how to find the Laplace transform of t².

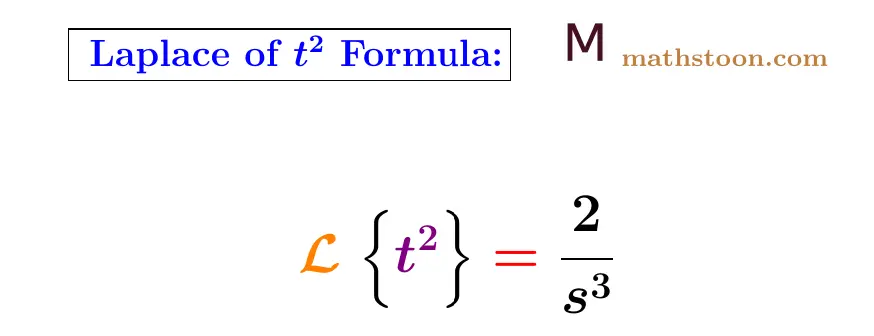
The Laplace transform t² (t square) is denoted by L{t²}, and its formula is given as follows:

L{t²} = 2/s³.

This follows from the Laplace formula of tⁿ: L{tⁿ} = n!/sⁿ⁺¹ by putting n=2.

Main Article: Laplace Transform: Definition, Table, Formulas, Properties & Examples

What is the Laplace Transform of t²?

Answer: The Laplace transform of t² is equal to 2/s³.

Proof:

The Laplace transform of f(t) by definition is given by

L{f(t)} = $\int_0^\infty$ f(t) e^-st dt.

So to find the Laplace transform of t² by definition, we need to follow below steps.

Step 1: Put f(t) = t².

Therefore,

L{t²} = $\int_0^\infty$ t² e^-st dt. …(I)

Step 2: In order to compute the above integral, let us use the theory of the Gamma function Γ(x) = $\int_0^\infty$ t^x-1 e^-t dx. Assume that

z=st

∴ dz=s dt ⇒ dt = dz/s. Also, t=z/s.

t	z
0	0
∞	∞

Step 3: The equation (I) then implies that

L{t²} = $\int_0^\infty \Big(\dfrac{z}{s} \Big)^2 e^{-z} \dfrac{dz}{s}$

= (1/s²⁺¹) $\int_0^\infty z^{2+1-1} e^{-z} dz$

= (1/s³) $\Gamma(2+1)$, by the definition of the Gamma function.

= (1/s³) × 2! as we know that Γ(n+1) = n!

= 2!/s³

= 2/s³.

Therefore, the Laplace transform of t^2 is equal to 2/s³ and this is proved by the definition of Laplace transforms.

Read Also:

Laplace Transform of eat:	The Laplace transform of eat is 1/(s-a).
Laplace transform of sin(at):	The Laplace transform of sin(at) is a/(s2+a2).
Laplace transform of cos(at):	The Laplace transform of cos(at) is s/(s2+a2).
Laplace transform of a constant:	The Laplace transform of a constant c is c/s.
Inverse Laplace transform of constant:	The inverse Laplace transform of c is cδ(t), where δ(t) is the Dirac delta function.

FAQs