SN Dey Class 11 Solutions Differentiation Short Answer Type Questions

Click here to get SN Dey Class 11 All Chapters Solutions

SN Dey Class 11 Differentiation Short Answer Type Questions Solutions

SN Dey class 11 Differentiation short answer type questions Ex 1 solutions:

Ex 1: Examine whether f(x)=|x+1| has a derivative at x=-1.

Solution:

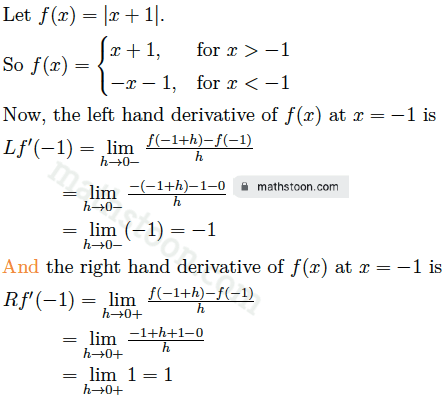
As $Lf'(-1) \neq Rf'(-1)$, we conclude that f(x)=|x+1| has no derivative at x=-1.

SN Dey class 11 Differentiation short answer type questions Ex 2 solutions:

Ex 2: If the derivative of f(x) at x=a is $f'(a)$, show that

$\lim\limits_{x \to a}\dfrac{xf(a)-af(x)}{x-a}$ $=f(a)-af(a)$

Solution:

SN Dey class 11 Differentiation short answer type questions Ex 3 solutions:

Ex 3: Find from the first principle, the derivatives of the following function:

Ex 3.(i): From the first principle, find the derivative of x³.

Solution:

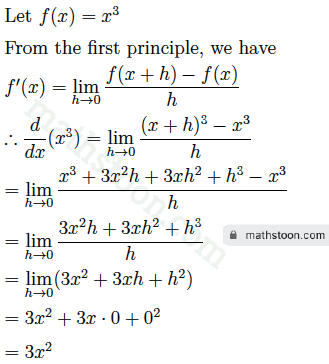
Ex 3.(ii): From the first principle, find the derivative of x⁶.

Solution:

Derivative of square root of x : The derivative of root x is 1/2√x.

Ex 3.(iii): From the first principle, find the derivative of √x.

Solution:

Ex 3.(iv): From the first principle, find the derivative of tan $\frac{x}{2}$.

Solution:

Ex 3.(v): From the first principle, find the derivative of sec 3x.

Solution:

Ex 3.(vi): From the first principle, find the derivative of sin 4x.

Solution:

Ex 3.(vii): From the first principle, find the derivative of sin x°.

Solution:

Ex 3.(viii): From the first principle, find the derivative of 1/√x.

Solution:

Ex 3.(ix): From the first principle, find the derivative of e^3x.

Solution:

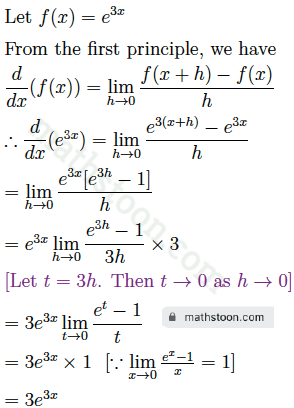
Ex 3.(x): From the first principle, find the derivative of ³√x.

Solution:

Ex 3.(xi): From the first principle, find the derivative of log 3x.

Solution:

Ex 4: Find from the definition of the differential coefficients of the following function:

Ex 4.(i): y=x+$\frac{1}{x}$ at x=1.

Solution:

Ex 4.(ii): y=4 at x=3.

Solution:

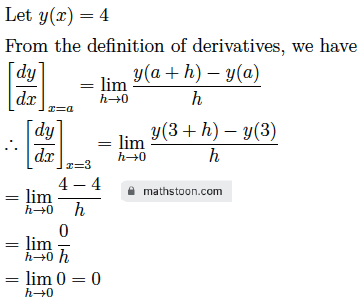
Ex 4.(iii): y=$\frac{1}{2x+3}$ at x=0.

Solution:

Ex 4.(iv): y=sec 2x at x=$\frac{\pi}{6}$.

Solution:

Ex 4.(v): y=√x at x=2.

Solution:

Ex 4.(vi): y=x^2/3 at $x=\frac{1}{27}$.

Solution:

Ex 4.(vii): y=e^-2x at x=0.

Solution:

Ex 4.(viii): y=cot $\frac{x}{2}$ at x=$\pi$.

Solution:

Ex 4.(ix): y=cos 2x at x=$\frac{\pi}{4}$.

Solution:

Ex 6: Differentiate the following functions with respect to x:

Ex 6.(i): 10^x ⋅ x¹⁰

Solution: The derivative of 10^x ⋅ x¹⁰ is equal to

d/dx(10^x ⋅ x¹⁰) = 10^x d/dx(x¹⁰) + x¹⁰ d/dx(10^x) , by the product rule of derivatives.

= 10^x ⋅ 10x^10-1 + x¹⁰⋅10^x log_e10

= 10^x+1 ⋅x⁹ + x¹⁰⋅10^x log_e10

Ex 6.(ii): x³log x

Solution:

d/dx(x³ log x) = x³ d/dx(log x) + log x d/dx(x³) 

= x³ ⋅ 1/x + log x ⋅ 3x²

= x² + 3x² log x 

= x² (1 + 3log x)

 

Ex 6.(iii): e^x tan x

Solution: The derivative of e^x tan x is equal to

d/dx(e^x tan x) = e^x d/dx(tan x) + tan x d/dx(e^x) , by the product rule of derivatives.

= e^x ⋅ sec²x + tan x ⋅ e^x

= e^x (tan x + sec²x)

 

Ex 6.(iv): √x log √x

Solution:

d/dx(√x log √x) = √x ⋅ d/dx(log √x) + log √x ⋅ d/dx(√x) 

$=\sqrt{x} \frac{1}{\sqrt{x}} \frac{d}{dx}(\sqrt{x})$ $+\log \sqrt{x} \frac{d}{dx}(\sqrt{x})$

$=\frac{d}{dx}(x^{1/2}) (1+\log \sqrt{x})$

$=\frac{1}{2} x^{1/2-1} (1+\log \sqrt{x})$

$=\frac{1}{2\sqrt{x}} (1+\log \sqrt{x})$

 

Ex 6.(v): (x²+1)e^x

Solution:

d/dx{(x²+1)e^x} = (x²+1) d/dx(e^x) + e^x d/dx(x²+1) 

= (x²+1) e^x + e^x (2x+0) 

= e^x (x²+1+2x)

= e^x (x+1)²

 

Ex 6.(vi): e^x sec x

Solution:

The derivative of e^x sec x is equal to

d/dx(e^x sec x) = e^x d/dx(sec x) + sec x d/dx(e^x) , by the product rule of derivatives.

= e^x ⋅ sec x tan x + sec x ⋅ e^x

= e^x sec x (tan x + 1)

Ex 6.(vii): (2x-5)(x²+2)

Solution:

Ex 6.(viii): cosec x ⋅ cot x

Solution:

The derivative of cosec x ⋅ cot x is equal to

d/dx(cosec x ⋅ cot x) = cosec x d/dx(cot x) + cot x d/dx(cosec x) , by the product rule of derivatives.

= cosec x ⋅ (-cosec² x) + cot x ⋅ (-cosec x cot x)

= -cosec x (cosec²x+cot²x)

 

Ex 6.(ix): (sin x +sec x)(cos x +cosec x)

Solution:

The derivative of (sin x +sec x)(cos x +cosec x) is equal to

d/dx[(sin x +sec x)(cos x +cosec x)]

= (sin x +sec x) d/dx(cos x +cosec x) + (cos x +cosec x) d/dx(sin x +sec x)

= (sin x +sec x) (-sin x -cosec x cot x) + (cos x +cosec x) (cos x +sec x tan x)

 

Ex 6.(x): sec³ x

Solution: The derivative of sec³x is equal to

d/dx(sec³ x) = 3 sec² x ⋅ d/dx(sec x)

= 3 sec² x ⋅ sec x tan x

= 3 sec³ x tan x

Ex 6.(xi): √xe^x sec x

Solution:

Ex 6.(xii): xtan x log x

Solution:

Ex 6.(xiii): x cos x + 2^x sec x

Solution:

The derivative of x cos x + 2^x sec x is equal to

d/dx(x cos x + 2^x sec x) = d/dx(x cos x) + d/dx(2^x sec x)

= x d/dx(cos x) + cos x d/dx(x) + 2^x d/dx(sec x) + sec x d/dx(2^x)

= x sin x + cos x ⋅ 1 + 2^x sec x tan x + sec x ⋅ 2^xlog_e2

= x sin x + cos x + 2^x sec x (tan x + log_e2)

 

Keywords: SN Dey Class 11 Differentiation Solutions | Solution of Class 11 Derivative | SN Dey Class 11 Solutions | SN Dey Class 11 Derivative Solutions Short Answer Type Questions | WB Board Class 11 Derivative Solution | SN Dey Class 11 Math Chapter Derivative Solution | Differentiation Short Answer Type Questions Answers | sn dey class 11 derivatives solutions