SN Dey Class 11 Solutions Differentiation Very Short Answer Type Questions

SN Dey Class 11 Differentiation Solutions | Solution of Class 11 Derivative | SN Dey Class 11 Solutions | SN Dey Class 11 Derivative Solutions Very Short Answer Type Questions | West Bengal Board Class 11 Derivative Solution | SN Dey Class 11 Math Chapter Derivative Solution | Differentiation Very Short Answer Type Questions Answers | sn dey class 11 derivatives solutions

Click here to get SN Dey Class 11 All Chapters Solutions

SN Dey Class 11 Differentiation Very Short Answer Type Questions Solutions

SN Dey class 11 Differentiation very short answer type questions Ex 1 solutions:

Ex 1: Define the derivative of a function f(x) at an arbitrary point x in its domain of definition.

Solution:

Let x be a point in the domain of the definition of f(x). The derivative of f(x) at a point x is given by the following limit:

$\lim\limits_{h\to 0}\dfrac{f(x+h)-f(x)}{h}$

and it is denoted by $f'(x)$.

SN Dey class 11 Differentiation very short answer type questions Ex 2 solutions:

Ex 2: Examine whether f(x)=|x| has a derivative at x=0.

Solution:

Let f(x)=|x|. We know that |x|=x if x>0 and |x|=-x if x $\leq$ 0. The left hand derivative of f(x) at x=0 is equal to

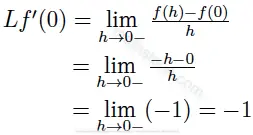
And the right hand derivative of f(x) at x=0 is equal to

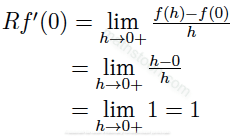
As the left hand derivative and the right hand derivative of f(x)=|x| at x=0 are not equal, we conclude that f(x)=|x| has no derivative at x=0. In other words,

$f'(0)$ does not exist.

SN Dey class 11 Differentiation very short answer type questions Ex 3 solutions:

Ex 3: If $y=\frac{1}{x}$, find $\frac{dy}{dx}$; also find the value of x for which dy/dx becomes undefined.

Solution:

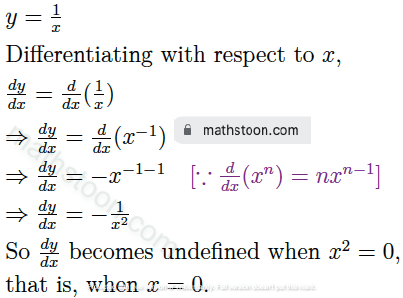
SN Dey class 11 Differentiation very short answer type questions Ex 4 solutions:

SN Dey class 11 Differentiation very short answer type questions Ex 5 solutions:

Ex 6: Differentiate the following functions w.r.t. x:

Ex 6(i): If y=x¹⁶ then find dy/dx.

Solution:

dy/dx= d/dx(x¹⁶)

= 16 x^16-1 by the power rule of derivatives.

= 16 x¹⁵

Ex 6(ii): If y=3x⁷ then find dy/dx.

Solution:

dy/dx= d/dx(3x⁷)

= 3 ⋅ 7x^7-1 by the power rule of derivatives.

= 21 x⁶

 

 

 

 

 

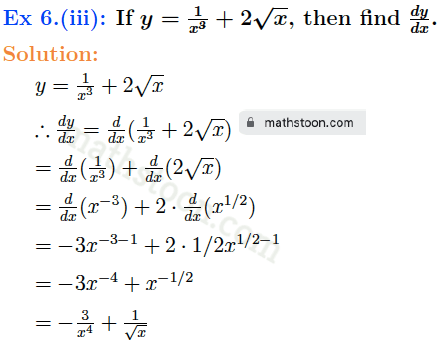
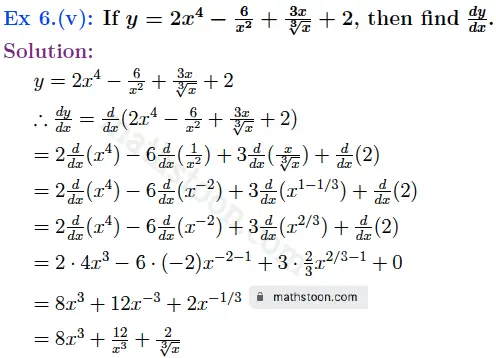
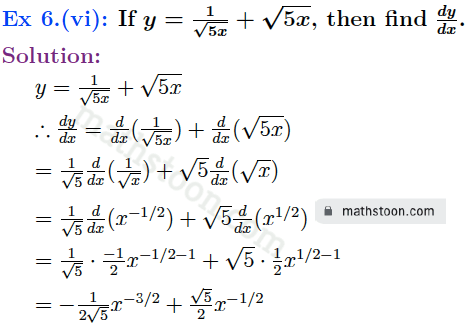
Ex 6(vii): If y=(x²-2)² then find dy/dx.

Solution:

dy/dx= d/dx{(x²-2)²}

= 2(x² -2) ⋅ d/dx(x²-2)

= 2(x² -2) ⋅ (2x-0)

= 4x(x² -2) 

 

 

Ex 6(ix): If y=(x²-2x)(x+1) then find dy/dx.

Solution:

dy/dx= d/dx{(x²-2x)(x+1)}

= (x² -2x) d/dx(x+1) + (x+1) d/dx(x² -2x), by the product rule of derivatives.

= (x² -2x)(1+0) + (x+1)(2x-2)

= x² -2x + 2x² +2x-2x-2

= 3x² -2x – 2

 

 

 

 

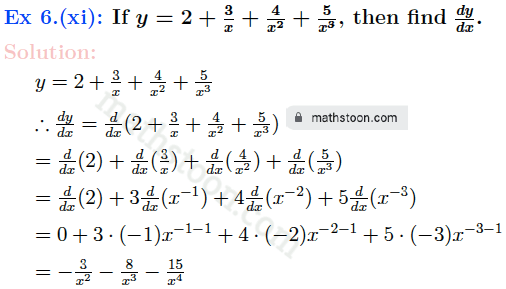
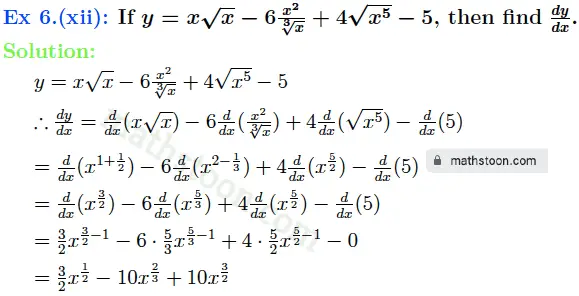
Ex 7: Find dy/dx :

Ex 7(i): If y=3log x -4√x+2e^x then find dy/dx.

Solution:

y = 3log x -4√x+2e^x

∴ dy/dx= d/dx(3log x -4√x+2e^x)

= 3 d/dx(log x) – 4 d/dx(√x)+2 d/dx(e^x)

= $3 \cdot \frac{1}{x}-$ 4 d/dx(x^1/2) + 2e^x

= $\frac{3}{x} – 4 \cdot \frac{1}{2}x^{1/2-1}$ + 2e^x

= $\frac{3}{x} -2x^{-1/2}$ + 2e^x

= $\frac{3}{x} -2x^{-1/2}$ + 2e^x

Ex 7(ii): If y = log₂ x  then find dy/dx.

Solution:

y = log₂ x 

∴ dy/dx= d/dx(log₂ x)

= d/dx(log₂ e ⋅ log_e x)  [∵ log_ab = log_ae ⋅log_eb]

= log₂ e ⋅ d/dx(log_e x)

= log₂ e ⋅ 1/x =1/x log₂e

Ex 7(iii): If y = 2x^m-3m^x+4e^x  then find dy/dx.

Solution:

y = 2x^m-3m^x+4e^x

∴ dy/dx= d/dx(2x^m-3m^x+4e^x)

= 2 ⋅ d/dx(x^m) – 3⋅ d/dx(m^x)+ 4⋅ d/dx(e^x)  

= 2 ⋅ mx^m-1 – 3⋅ m^x log_em + 4⋅ e^x

= 2mx^m-1 – 3m^x log_em + 4e^x

Ex 7(iv): If y = 2^x+2 -e^x+1 +3log 2x  then find dy/dx.

Solution:

y = 2^x+2 -e^x+1 +3log 2x

∴ dy/dx= d/dx(2^x+2 -e^x+1 +3log 2x)

= d/dx(2^x+2) – d/dx(e^x+1)+ 3⋅ d/dx(log 2x)  

= 2^x+2 ⋅ log_e2 ⋅ d/dx(x+2) – e^x+1 ⋅d/dx(x+1) + $3\cdot \frac{1}{2x}\cdot$ d/dx(2x) 

= 2^x+2 log_e2 ⋅ 1 – e^x+1 ⋅1 + $3\cdot \frac{1}{2x}\cdot$ 2 

= 2^x+2 log_e2 – e^x+1 + $\frac{3}{x}$ 

Ex 7(v): If y = log₁₀ x +10^x +x¹⁰+10  then find dy/dx.

Solution:

y = log₁₀ x +10^x +x¹⁰+10

∴ dy/dx= d/dx(log₁₀ x +10^x +x¹⁰+10)

= d/dx(log₁₀ x) +d/dx(10^x) + d/dx(x¹⁰) +d/dx(10)

= $ \frac{1}{x}$ log₁₀e + 10^xlog_e10 + 10 x^10-1 + 0

= $ \frac{1}{x}$ log₁₀e + 10^xlog_e10 + 10x⁹ 

Ex 7(vi): If y = e^x+1 -5^x+1 +e^{log x}+log_ax +log x^a  then find dy/dx.

Solution:

y = e^x+1 -5^x+1 +e^{log x}+log_ax +log x^a

∴ dy/dx= d/dx(e^x+1 -5^x+1 +e^{log x}+log_ax +log x^a)

= d/dx(e^x+1) -d/dx(5^x+1) + d/dx(x) +d/dx(log_ax) +d/dx(log x^a)  [∵ e^{log x} = x]

= e^x+1 d/dx(x+1) – 5^x+1 log_e5 ⋅ d/dx(x+1) + 1 + $\frac{1}{x}$ log_ae +ax^a-1 d/dx(x^a) 

= e^x+1(1+0) – 5^x+1 log_e5 ⋅(1+0) + 1 + $\frac{1}{x}$ log_ae + $\frac{1}{x^a}$ ax^a-1

= e^x+1 – 5^x+1 log_e5 + 1 + $\frac{1}{x}$ log_ae + $\frac{a}{x}$

Ex 7(vii): If y = a sec x + b tan x – c cosec x + d cot x -e  then find dy/dx.

Solution:

y = a sec x + b tan x – c cosec x + d cot x -e

∴ dy/dx= d/dx(a sec x + b tan x – c cosec x + d cot x -e)

= d/dx(a sec x) + d/dx(b tan x) – d/dx(c cosec x) + d/dx(d cot x) – d/dx(e)

= a d/dx(sec x) + b d/dx(tan x) -c d/dx(cosec x) +d d/dx(cot x) – 0

= a sec x tan x + b sec²x +c cosec x cot x -d cosec²x

 

 

 

 

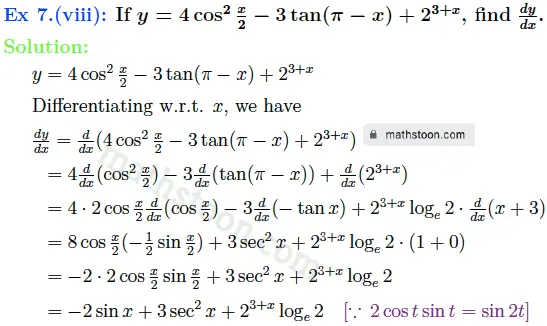
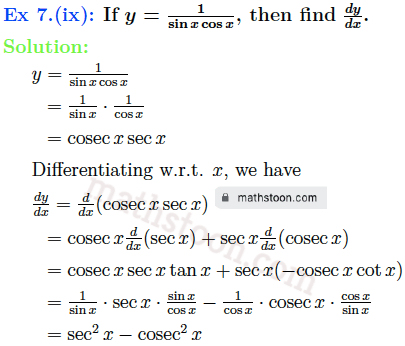
SN Dey class 11 Differentiation very short answer type questions Ex 8 solutions:

Ex 8: Find the derivative of cot x by expressing it in the form cos x ⋅ cosec x.

Solution:

SN Dey class 11 Differentiation very short answer type questions Ex 9 solutions:

SN Dey class 11 Differentiation very short answer type questions Ex 10 solutions:

SN Dey class 11 Differentiation very short answer type questions Ex 11 solutions:

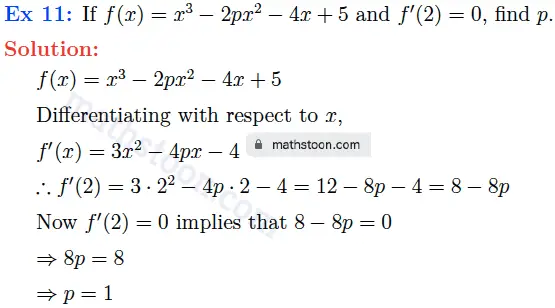
SN Dey class 11 Differentiation very short answer type questions Ex 12 solutions:

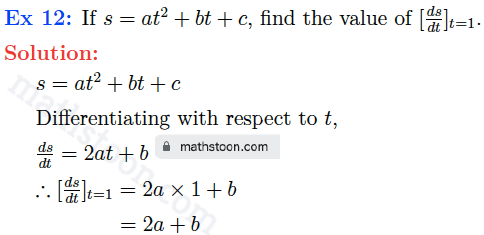
SN Dey class 11 Differentiation very short answer type questions Ex 13 solutions:

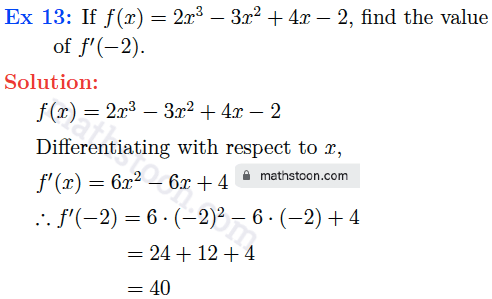
SN Dey class 11 Differentiation very short answer type questions Ex 14 solutions:

Ex 14: If $y=x^5$, show that $x \frac{dy}{dx}-5y=0$.

Solution:

 

 

 

 

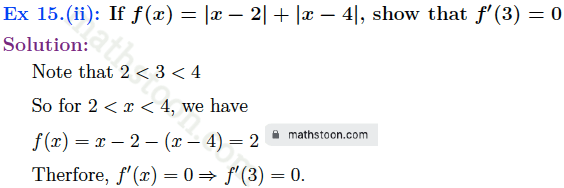
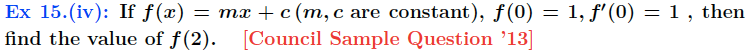
Solution:

Given f(x)=mx+c

∴ f(0) = m⋅0+c =c

So f(0)=1 implies that c=1

∴ f(x) = mx+1

Differentiating f(x) with respect to x, we get that

$f'(x) = m$

Now $f'(0)=1$ implies that m=1

Thus, f(x)=x+1

∴ f(2) = 2+1 =3