Derivative of sec x: Formula, Proof by First Principle, Chain, Quotient Rule

The derivative of sec x with respect to x is equal to secx tanx. The secx is the reciprocal of cosx. In this post, we will learn how to find the derivatives of sec x using the following methods:

• First principle of derivatives
• Chain rule of derivatives
• Quotient rule of derivatives.

What is the Derivative of Sec x?

The derivative of secx with respect to x is denoted by the symbol $\frac{d}{dx}$(sec x) or (sec x)$’$ and it is equal to secx tanx. Using the fact $\sec x =\frac{1}{\cos x}$, we can find the derivative of sec x by the chain rule and quotient rule of derivatives.

Derivative of Sec x Formula

The formula for the derivative of secx is given below.

• $\frac{d}{dx}$(sec x) = sec x tan x, (or)
• (sec x)$’$ = sec x tan x.

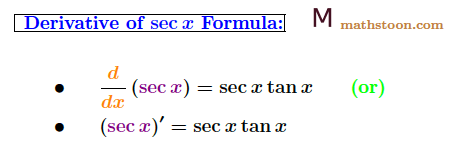
Derivative of Sec x by First Principle

We will show that the differentiation of sec x is sec x tan x by the first principle. Putting f(x) = sec x in the derivative formula by first principle $f'(x)$ $=\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}$, we get the derivative of sec x. Therefore,

Derivative of Sec x by Chain Rule

By the chain rule, we will now show that the differentiation of sec x is sec x tan x. We have

$\sec x =\dfrac{1}{\cos x}$

Put t=cosx. So $\dfrac{dt}{dx}=-\sin x$. Now,

$\dfrac{d}{dx}(\sec x)=\dfrac{d}{dx}(\dfrac{1}{\cos x})$

= $\dfrac{d}{dt}(\dfrac{1}{t}) \cdot \dfrac{dt}{dx}$, by the chain rule of derivatives

= $\dfrac{d}{dt}$(t^-1) ⋅ (-sinx)

= -t^-1-1 ⋅ (-sinx) by the power rule of derivatives

= $\dfrac{\sin x}{\cos^2 x}$ as t=cosx.

= secx tanx.

So the derivative of secx by chain rule is secx tanx.

Also Read:

Derivative of tanx	The derivative of tanx is sec2x.
Derivative of cotx	The derivative of cotx is -cosec2x.
Derivative of sin2x	The derivative of sin2x is 2sinx cosx.
Derivative of ecosx	The derivative of ecosx is -sinx ecosx.

Derivative of Sec x by Quotient Rule

We will now find the derivative of secx by the quotient rule. This rule is used to find the derivative of a quotient function which says that

$(\dfrac{f}{g})’=\dfrac{gf’-fg’}{g^2}$, where $’$ denotes the first order derivative.

Let us express secx as a quotient function as follows.

$\sec x =\dfrac{1}{\cos x}$

Applying the above quotient rule of derivatives with f=1 and g=cosx, we get that

$(\sec x)’ =\dfrac{\cos x \cdot 1^\prime – 1 \cdot (\cos x)’}{\cos^2 x}$

= $\dfrac{\cos x \cdot 0 – 1 \cdot (-\sin x)}{\cos^2 x}$

= $\dfrac{\sin x}{\cos^2 x}$ = secx tanx.

So the derivative of secx by quotient rule is secx tanx.

FAQs on Derivative of Sec x