Derivative of x^x: Formula, Proof by First Principle

The derivative of x^x (x to the power x) is equal to x^x(1+log_ex). In this post, we will learn the formula for the derivative of x^x and how to find it. To calculate the derivative of x to the x, we will use the following methods:

• Logarithmic differentiation
• First principle of derivatives.

Derivative of x^x Formula

The derivative of x^x is denoted by $\dfrac{d}{dx}$(x^x) or (x^x)$’$. The formula of the derivative of x^x is given as follows.

$\dfrac{d}{dx}$(x^x) = x^x(1+lnx),

where ln denotes the natural logarithm (log with base e), that is, lnx=log_ex.

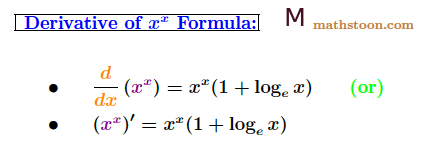
Derivative of x^x by Logarithmic Differentiation

Note that we use the logarithmic differentiation method to find the derivative of a function having another function as an exponent. Thus, we can find the derivative of x to the power x using this method. Let us put

y=x^x

Taking logarithms with base e both sides, we obtain that

log_e y = log_e x^x

⇒ log_e y = xlog_e x by the logarithm rule log_ab^k = k log_ab.

Differentiating both sides w.r.t. x, we get that

d/dx(log_e y) = d/dx(xlog_e x)

⇒ $\dfrac{1}{y} \dfrac{dy}{dx}$ = x d/dx(log_e x) + log_ex d/dx(x) by the product rule of derivatives.

⇒ $\dfrac{1}{y} \dfrac{dy}{dx}$ = x ⋅ 1/x + log_ex ⋅ 1

⇒ $\dfrac{dy}{dx}$ = y(1 + log_ex)

⇒ $\dfrac{dy}{dx}$ = x^x(1 + log_ex) as y=x^x.

So the derivative of x^x (x to the x) is equal to x^x(1 + log_ex) and this is obtained by the logarithmic differentiation.

Also Read: Derivative of 1/x

Derivative of 1/x² | Derivative of 1/x³

Derivative of x^x by First Principle

The derivative of f(x) by the first principle, that is, by the limit definition is given by

$\dfrac{d}{dx}(f(x))$$=\lim\limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$ $\cdots$ (I)

We will use the following fact:

$\lim\limits_{h\to 0}\dfrac{x^h-1}{h}=y$ if and only if $x=\lim\limits_{n\to\infty}\left(1+\dfrac yn\right)^n$ if and only if $x=e^y \iff y=\log(x)$

Put f(x)=x^x in the above formula (I). Thus we have:

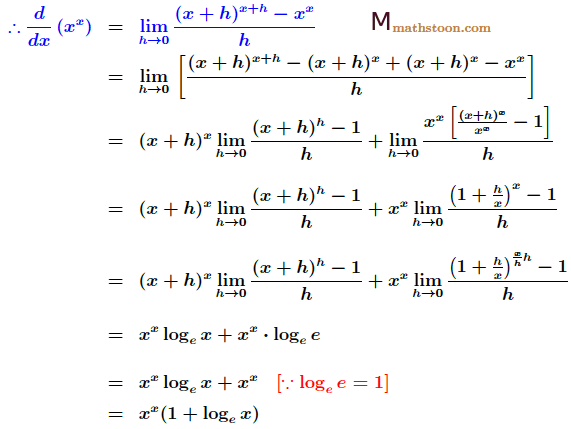
Thus, the derivative of x^x is x^x(1+log_ex) and this is obtained by the first principle of derivatives, that is, by the limit definition of derivatives.

Must Read:

Limit: Definition, Formulas, Examples

Continuity of a Function

Discontinuity of a Function

Derivative: Definition, Formulas, Examples

Integration: Definition, Formulas, Examples

FAQs on Derivative of x^x