The Laplace transform of sin^2t is equal to 1/2s – s/(2s2+8). In this article, we will learn how to find the Laplace of sin square t. The formula of the Laplace of sin2t is given below:
L{sin2t} = 1/2s – s/(2s2+8).
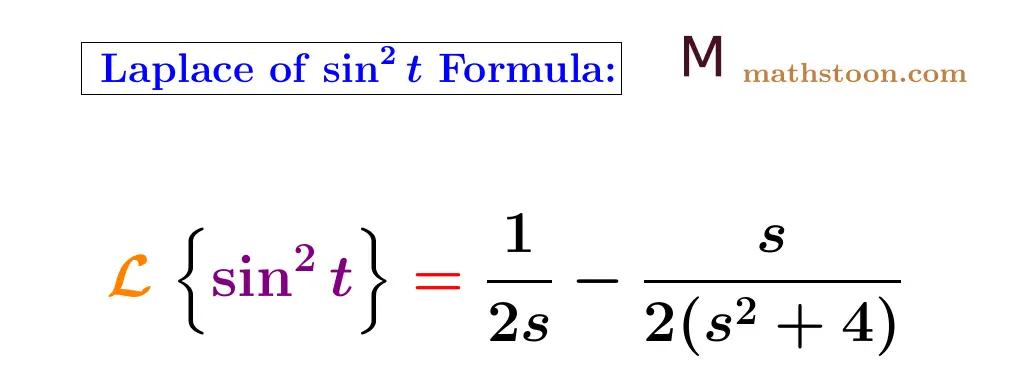
Table of Contents
Find the Laplace Transform of sin2t
Answer: The Laplace transform of sin square t is 1/2s – s/(2s2+8).
Proof:
It is known from trigonometry that 1-cos2t=2sin2t. Therefore, we have
sin2t = $\frac{1}{2}$(1-cos2t)
Now, we take the Laplace transforms on both sides of the above equation. By doing so, we get that
L{sin2t} = L{$\frac{1}{2}$(1-cos2t)}.
Applying the linearity property of Laplace transforms,
L{sin2t} = $\frac{1}{2}$ (L{1} – L{cos2t}).
We know that the Laplace Transform of 1 is 1/s and the Laplace transform of cos 2t is s/(s2+4). Hence, it follows that
L{sin2t} = $\dfrac{1}{2} \left(\dfrac{1}{s}-\dfrac{s}{s^2+4} \right)$
Simplifying we obtain that
L{sin2t} = $\dfrac{1}{2s}-\dfrac{s}{2(s^2+4)}$
Therefore, the Laplace transform of sin^2t is equal to 1/2s – s/(2s2+8).
Main Article: Laplace Transform: Definition, Table, Formulas, Properties
Laplace tansform of a constant
FAQs
Answer: The Laplace transform of sin^2t is equal to 1/2s – s/(2s2+8). That is, L{sin2t} = 1/2s – s/(2s2+8).
This article is written by Dr. T. Mandal, Ph.D in Mathematics. On Mathstoon.com you will find Maths from very basic level to advanced level. Thanks for visiting.