The Laplace transform of t sint is 2s/(s2+1)2, that is, L{t sint}=2s/(s2+1)2. The function t sint is the product of t and the sine of t. In this article, we will find the Laplace transform of both t sint and t sin(at).
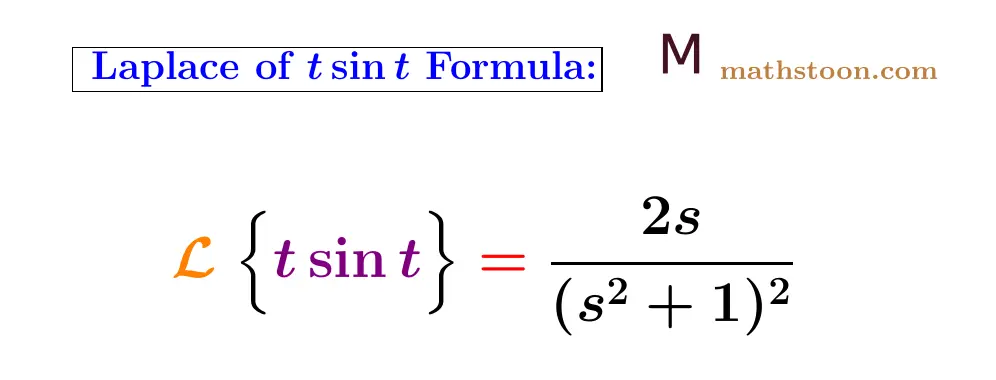
Table of Contents
What is the Laplace Transform of t sin(t)?
Answer: The Laplace transform of t sin t is 2s/(s2+1)2.
Proof:
To find the Laplace transform of t sin(t), we will use the formula for the Laplace transform of a function f(t) multiplied by t, denoted by L{t f(t)}, which is given by the following formula: (multiplication by t Laplace transform formula)
$L\{t f(t)\} = – \dfrac{d}{ds}(F(s))$, where L{f(t)}=F(s) …(∗)
Step 1: Put f(t) = sin t in the above formula.
∴ F(s) = L{f(t)} = L{sin t} = 1/(s2+1).
Step 2: So the Laplace transform of tsin(t) by (∗) is equal to
$L\{t\sin t\} = – \dfrac{d}{ds}\left(\dfrac{1}{s^2+1}\right)$
Step 3: By quotient rule of derivatives, we obtain that
$L\{t\sin t \}$ $= – \dfrac{(s^2+1)\frac{d}{ds}(1)-1 \frac{d}{ds}(s^2+1)}{(s^2+1)^2}$
$= – \dfrac{(s^2+1)\cdot 0- 1\cdot 2s}{(s^2+1)^2}$
$= – \dfrac{-2s}{(s^2+1)^2}$
$= \dfrac{2s}{(s^2+1)^2}$.
So the Laplace transform of tsin t is 2s/(s2+1)2.
| Find the Laplace transform of t sint. Summary: L{t sin t} = 2s/(s2+1)2. |
Also Read:
| Laplace transform of t: | 1/s2 |
| Laplace transform of sin t: | 1/(s2+1) |
| Laplace transform of sin(t)/t: | tan-1(1/s) |
| Laplace transform of cos t: | s/(s2+1) |
| Laplace transform of t cost: | (s2-1)/(s2+1)2 |
| Laplace transform of cos(t)/t: | Does Not Exist |
What is the Laplace Transform of t sin(at)?
Answer: The Laplace transform of t sin at is 2as/(s2+a2)2.
Proof:
Put f(t) = t sin(at) in the above formula (∗).
Note that L{sin at} = a/(s2+a2). So the Laplace transform of t sin(at) by the above formula (∗) is equal to
$L\{t\sin(at)\} = – \dfrac{d}{ds}\left(\dfrac{a}{s^2+a^2}\right)$
$= – \dfrac{(s^2+a^2)\frac{d}{ds}(a)-a \frac{d}{ds}(s^2+a^2)}{(s^2+a^2)^2}$
$= – \dfrac{(s^2+a^2)\cdot 0-a \cdot 2s}{(s^2+a^2)^2}$
$= – \dfrac{-2as}{(s^2+a^2)^2}$
$= \dfrac{2as}{(s^2+a^2)^2}$.
So the Laplace transform of tsin at is 2as/(s2+a2)2.
| Laplace transform of e-t | 1/(s+1) |
| Laplace transform of 1 | 1/s |
| Laplace transform of 1/t | Not Exist |
FAQs
Answer: The Laplace transform of the product tsint is 2s/(s2+1)2, that is, L{t sin t} = 2s/(s2+1)2.
Answer: The Laplace transform of the product tsinat is 2as/(s2+a2)2, that is, L{t sin at} = 2as/(s2+a2)2.
This article is written by Dr. T. Mandal, Ph.D in Mathematics. On Mathstoon.com you will find Maths from very basic level to advanced level. Thanks for visiting.