The Laplace transform of tet is equal to 1/(s-1)2. In this article, we will learn how to find the Laplace transform of the product function tet.
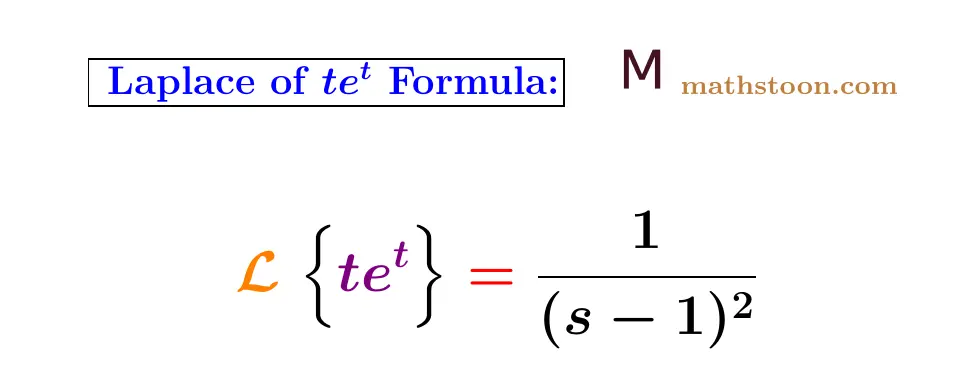
Table of Contents
What is the Laplace Transform of tet?
Answer: The Laplace transform of tet is 1/(s-1)2 when s>1.
Proof:
We will find the Laplace transform of tet by definition. Recall the definition of the Laplace transform of f(t) which is given below:
L{f(t)} = $\int_0^\infty$ f(t) e-st dt.
Put f(t) = tet.
∴ L{tet} = $\int_0^\infty$ tet e-st dt
= $\lim\limits_{T\to \infty} \int_0^T$ t e-(1-s)t dt
Using integrating by parts formula, the above is
= $\lim\limits_{T\to \infty} \Big( \left[ t \cdot \dfrac{e^{(1-s)t}}{1-s} \right]_{t=0}^T$ $- \int_0^T \dfrac{e^{(1-s)t}}{1-s} \, dt\Big)$
= $\dfrac{1}{1-s} \lim\limits_{T \to \infty} \Big(T e^{(1-s)T}$ $- \int_0^T e^{(1-s)t} \, dt\Big)$
= $\dfrac{1}{s-1} \lim\limits_{T \to \infty} \int_0^T e^{(1-s)t} \, dt$ [as s>1, we have e(1-s)T →0 when T→∞]
= $\dfrac{1}{s-1} \lim\limits_{T \to \infty} \Big[ \dfrac{e^{(1-s)t}}{1-s} \Big]_{t=0}^T$
= $\dfrac{1}{s-1} \lim\limits_{T \to \infty} \Big[ \dfrac{e^{(1-s)T}}{1-s} – \dfrac{1}{1-s} \Big]$
= $\dfrac{1}{s-1} \Big[ 0 – \dfrac{1}{1-s} \Big]$
= $\dfrac{1}{(s-1)^2}$
So the Laplace transform of tet by definition is 1/(s-1)2.
| Find the Laplace transform of tet. Summary: L{t et} = 1/(s-1)2. |
Also Read:
| Laplace transform of sin t: | 1/(s2+1) |
| Laplace transform of cos t: | s/(s2+1) |
| Laplace transform of e-t: | 1/(s+1) |
| Laplace transform of 1: | 1/s |
Prove that Laplace of tet is 1/(s-1)2.
Proof:
Recall the multiplication by tn Laplace transform formula, we have that:
$L\{t f(t)\} = – \dfrac{d}{ds}(F(s))$, where L{f(t)}=F(s)
Put f(t) = et. Note that F(s) = L{et}=1/(s-1).
Then L{tet} = $- \dfrac{d}{ds}\left( \dfrac{1}{s-1} \right)$
= $- \left(- \dfrac{1}{(s-1)^2} \right)$
= $\dfrac{1}{(s-1)^2}$.
Thus, the Laplace of tet is 1/(s-1)2.
Laplace of tet by Differentiation
We prove that the Laplace of tet is 1/(s-1)2.
Proof:
We know that the Laplace transform of first derivative of f(t) is given as follows:
$L\{f'(t)\}=f(0)+s L\{f(t)\}$ …(I)
Let f(t) = tet
Then we have from (I) that
L{et+tet} = 0+sL{tet}
By the linearity of Laplace transform, we get that
L{et} + L{tet} = s L{tet}
⇒ L{et} = (s-1) L{tet}
⇒ 1/(s-1) = (s-1) L{tet} as the Laplace of et is 1/(s-1).
⇒ L{tet} = 1/(s-1)2.
Thus, we prove that the Laplace transform of tet by first derivative formula is equal to 1/(s-1)2.
FAQs
Answer: The Laplace of tet is 1/(s-1)2.
Answer: The Laplace of et is 1/(s-1).
