The Laplace transform of e^-t sint, that is, L{e-t sint} is equal to 1/[(s+1)2+1]. Note e-t sint is a product of two functions, and its Laplace is calculated using the first shifting property of Laplace transforms.
The Laplace formula of e-t sint is given below.
| L{e-t sint} = 1/[(s+1)2+1]. |
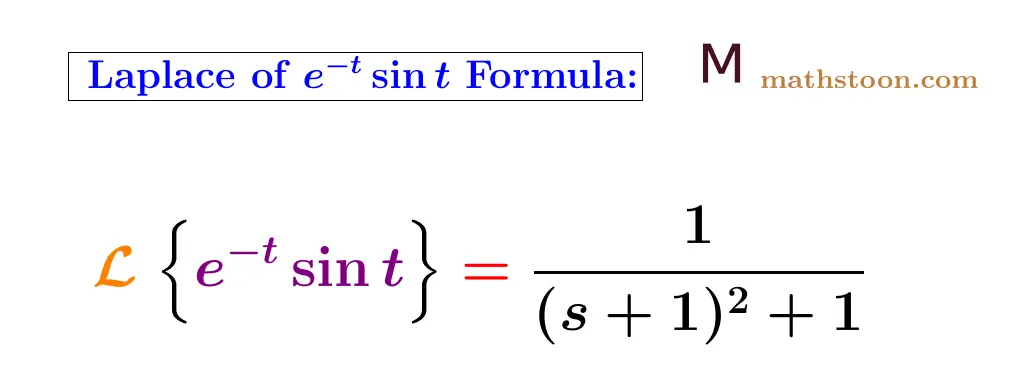
Table of Contents
Laplace of e-t sint
Answer: The Laplace of e-t sint is 1/[(s+1)2+1].
Explanation:
Step 1: First, we calculate the Laplace of sint using the formula of L{sinat}.
L{sint} = $\dfrac{1}{s^2+1}$.
Step 2: Now use the first shifting property of Laplace transforms which says that if L{f(t)} = F(s), then
L{eat f(t)} = F(s-a).
Step 3: In our case, a=-1 and f(t) = sint. So F(s) = $\dfrac{1}{s^2+1}$.
Thus, L{e-t sint} = F(s+1) = $\dfrac{1}{(s+1)^2+1}$.
That is, L{e-t sint} = $\dfrac{1}{s^2+2s+2}$.
So the Laplace transform of e-t sint is equal to 1/(s2+2s+2), and this is obtained by using the first shifting property of Laplace transforms.
More Laplace Transforms:
Laplace transform of (1-sint)/t
Laplace transform of (1-cost)/t
FAQs
Answer: The Laplace transform of e-t sint is equal to 1/(s2+2s+2).
This article is written by Dr. T. Mandal, Ph.D in Mathematics. On Mathstoon.com you will find Maths from very basic level to advanced level. Thanks for visiting.